재귀함수, 하노이의 탑
📝 백준 1914번
큰 규칙은 가장 큰 원판을 시작 기둥에서 목표기둥으로 옮기는데 있다.
이는 하노이의 탑 규칙을 지키기위해 구상하다보니 생긴 원리!
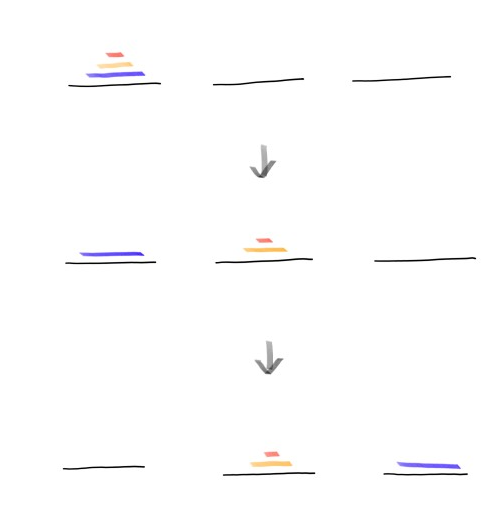
규칙 1,2를 만족하면서 원판들을 옮기기 위해서는 가장 큰 원판이 시작기둥에서 목표기둥으로 옮겨야 한다.
📝 선행작업, 후행작업
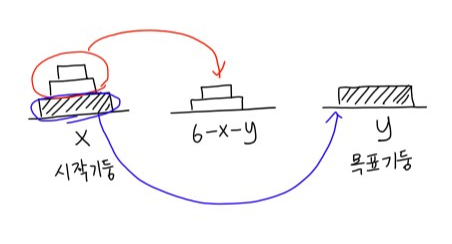
최소 이동으로 원판들을 옮기려면,
1. 가장 큰 원판을 제외한 나머지 원판들이 크기 순으로 중간기둥으로 옮겨져 있어야 한다.
→ 이를 위해서는 가장 큰 원판을 옮기기 전에 나머지 원판들이을 중간기둥으로 옮기는 선행 작업이 되어있어야 한다는 의미이다.
2. 가장 큰 원판을 시작기둥에서 목표 기둥으로 옮긴다.(목표작업)
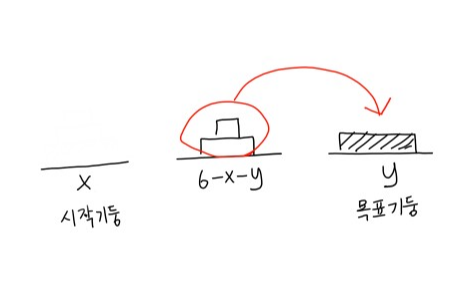
3. 중간 기둥에 옮겨져 있는 원판 역시 목표기둥으로 옮기는 후행 작업을 하면 된다.
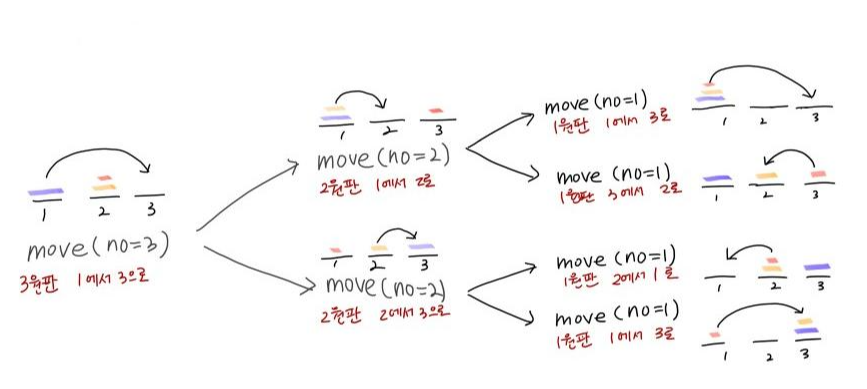
원판 3개가 있다고 가정하고 위의 과정을 되돌아 보자!
즉, 가장 큰 원판(3)을 시작기둥(x)에서 목표기둥(y)으로 옮기기 위해서는 나머지원판(1,2)가 시작기둥(x)에서 중간 기둥(6-x-y)으로 옮겨져 있어야한다. 그리고 나서 가장 큰 원판(3)을 시작기둥(x)에서 목표기둥(y)로 옮길 수 있다.
그 뒤 나머지 원판(1,2)을 중간기둥(6-x-y)에서 목표기둥(y)로 옮기는 작업을 하면 된다.
# 선행 작업
1원판을 1에서 3로 옮김
2원판을 1에서 2로 옮김
1원판을 3에서 2로 옮김
3원판을 1(시작기둥)에서 3(목표기둥)로 옮김
# 후행 작업
1원판을 2에서 1로 옮김
2원판을 2에서 3로 옮김
1원판을 1에서 3로 옮김↓
# 선행 작업
1원판을 1(시작기둥)에서 3(중간기둥)로 옮김
2원판을 1(시작기둥)에서 2(목표기둥)로 옮김(print)
# 후행작업
1원판을 3(중간기둥)에서 2(목표기둥)로 옮김
# -----------------------------
3원판을 1에서 3로 옮김(print)
# -----------------------------
# 선행 작업
1원판을 2(시작기둥)에서 1(중간기둥)로 옮김
2원판을 2(시작기둥)에서 3(목표기둥)로 옮김(print)
# 후행작업
1원판을 1(중간기둥)에서 3(목표기둥)로 옮김
📝 제출용 코드
# 즉 move(N)은 두번의 move(N-1) 재귀 과정을 수반한다.
# 파라미터 값
# 현재 옮겨야하는 원판 번호 no
# 시작 기둥 x
# 목표 기둥 y
# 중간 기둥 6-x-y
import sys
def move(no, x, y):
if no == 0:
return
# 선행작업
# 시작 기둥에서 중간 기둥으로 이동
move(no-1, x, 6-x-y)
print(f'{no}원판을 {x}에서 {y}로 옮김') # 시작기둥에서 목표 기둥으로 옮김.
# print(f'{x} {y}')
# 후행작업
# 중간기둥에서 목표기둥으로 이동
move(no-1, 6-x-y, y)
n = int(sys.stdin.readline().rstrip())
# n이 20보다 큰 경우에는 과정을 출력할 필요 없다.
if n > 20:
# 최소 이동 횟수는 2^n-1
print(2**n-1)
else:
print(2**n-1)
move(n, 1, 3)이러한 규칙을 알면 하노이의 탑 이동횟수를 구하는 공식은 자동으로 이해된다.
하노이의 탑에서 이용한 재귀를 genuinely재귀(순수한 재귀)라고 한다.
함수 내 재귀 호출을 여러번 수행하는 함수!
def recur(n: int) -> int:
if n > 0:
recur(n-1)
print(n)
recur(n-2)
recur(4)
# recur(4) -> recur(3) 실행 된 후에, print(4), 그 후에 recur(2) 실행.
# recur(3) -> recur(2) 실행 된 후에, print(2), 그 후에 recur(1) 실행.참고한 책 : Do it, 자료구조와 함께 배우는 알고리즘 입문
참고한 블로그 : https://mgyo.tistory.com/185
'하노이의 탑' 이해하기 (feat. 재귀 함수)
들어가며 하노이의 탑 문제 소개 문제 정의 아이디어 얻기 아이디어 재귀 출발점, 도착점, 경유점 문제 분해 실제 코드 번외 : 원반의 개수에 따른 총 이동횟수 구하기 마무리 자료 출처 https://www
mgyo.tistory.com
'알고리즘' 카테고리의 다른 글
| 자료구조, Binary Search Tree (0) | 2023.04.02 |
|---|---|
| 자료 구조, Linked List (0) | 2023.04.02 |
| DFS 관련 연산 문제 (0) | 2023.03.07 |
| 백준 1260번 DFS, BFS (0) | 2023.03.06 |
| 데일리 알고리즘 230120 (0) | 2023.01.22 |


